|
On the basis of the regularity of the transmission of the
X-Y chromosomes and the ancestral structure of sexual beings,
typical splitting proportions can be postulated as inheritance
probability values in the ascendance. |
||||||||||||||||||||||||||
|
Over six decades have passed since Thomas Hunt Morgan (1866-1945)
and his co-worker Calvin B. Bridges (1889-1938) discovered sex-linked
inheritance in the fruit fly Drosophilia melanogaster, "the
geneticist's pet". In 1916 Morgan was able to announce:
"We now know how the factors of heredity carried by the
parents are sorted out to the germ cells".
This will result in different inheritance probabilities for
the individual relationship lines. This will be explained by
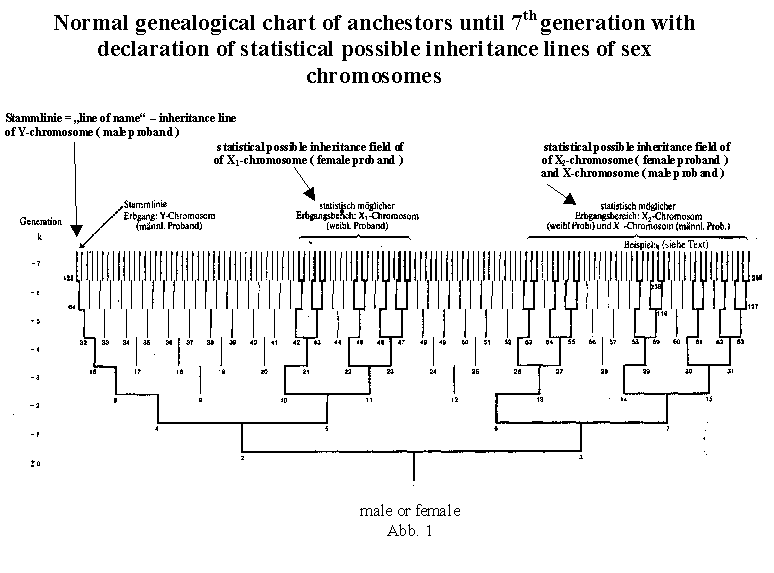
the example of a human genealogical table. A male person, for example the proband number 1 himself, receives his X chromosome with certainty (probability 1) from his mother (number 3) only. She herself, however, inherited this chromosome either from her father (number 6) or from her mother (number7), and with equal probability, so that both probability values are halved in the transmission to the next generation (see table 2). Therefore the probability is 0.5 for each. From ancestor number 6 the probability value does not chance in the transmission to the next generation, since ancestor number 6, as a male. can receive his X chromosome only from his mother (number 13); the probability of number 13 therefore remains 0.5. While for the female ancestor number 7, parents number 14 and number 15 come into play as transmitters with equal probability, the probability values therefore are halved again in the transmission to the next ancestral generation (probability of number 14 and number 15 is 0.25 each). This will suffice as a description of disproportionization. The Y chromosome, always passed only from father to son, has a completely unambiguous inheritance line on the genealogical chart. The probability value for the Y chromosome within the principal line is therefore always 1, independent of the generation. If, for example, in the case of a great-grandson, the entire legacy has disappeared in the individual case, his Y chromosome still remains fully preserved. In table 2, the probability values are given for all ancestors up to the generation k = -6. The nomenclature is that of today's scholarly genealogy. Naturally the b values in the chart for the X chromosome (bx for the man, bx1 and bx2 for the woman) are always 0 or 1 [because of crossing over, 0 or 1 is valid stritcly speaking only for single genes, which are localized on the X chromosome!] in the individual case, namely 1 only once in each ancestral generation (in the case of one ancestor) and 0 in all other positions (note 10). Those positions on the genealogical chart marked with a line in table 2 are eliminated for an inheritance probability of the sex chromosomes on the basis of the X-Y mechanism. There are "free places" and "new" areas in each higher ancestral generation. The percentage of "free places" becomes increasingly bigger within the chart as one goes back in time. The "free places" can in given cases be filled in the case of multiple inheritance (for example, ancestor 12, if the same as ancestor 10, (if ancestor 6 and 7 are brother and sister) female proband; see illustration 3c). Such ancestral charts, which show loss of ancestors, also called ancestral implex, will, however, not be looked at more closely in these basic considerations within the first ancestral generations. Admittedly, loss of ancestors will be the rule in higher generations, and the "pure" numerical relationships will be obscured, partially through "shifting of generations", such as niece-uncle marriages. In our civilization, marriages of close relatives are no rarities.
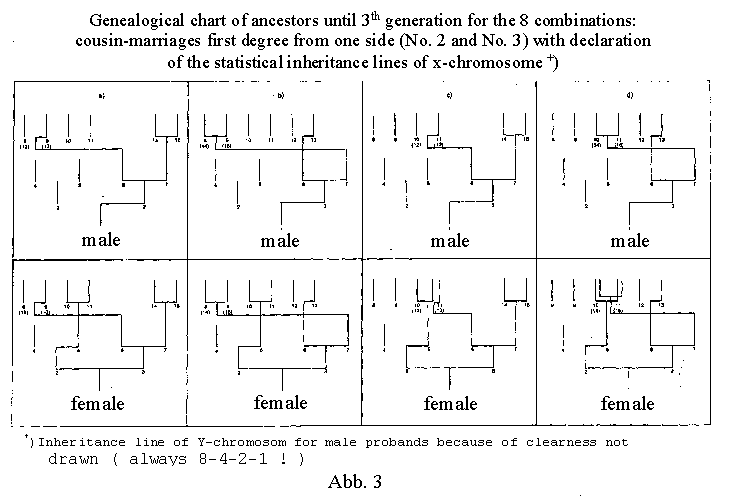
The eight different possible combinations of a cousin-aunt marriage
of the first degree on one side are shown in figure 3 a-d and
figure 4 (here there are only six rather than eight different
great-grandparents!). Figure 4 gives all inheritance probability
values for these eight combinations, limited to the third generation,
k = -3. All possible inheritance lines for the sex chromosomes for seven generations can be seen clearly in figure 1. It is differentiated between male and female probands. For the individual inheritance case of the X chromosomes designated x1 and x2 it is a question of only one single line. For example, for x2 , such a line is 238-119-59-29-14-7-3-1. Moreover, from the seventh generation on, there are twenty additional inheritance lines, some with greater, some with lesser statistical probability. From the two illustrations it is clear that there are basic differences between ancestral charts with male and female probands. The author is not aware that this fact has been referred to previously in the scientific literature. The genealogical table of a male proband is characterized on the one hand by the clear transmission of the Y chromosome within the so-called male line, and on the other hand by the inheritance probability field of the single X chromosome. The genealogical table of a female proband is characterized by two independent inheritance probability fields for the two X chromosomes (X1 and X2). Thus the X2 field of a female proband is identical with the X field of a male proband. The possible inheritance paths for the eight combinations
of cousin marriages to the third generation can be seen in illustration
3, where only the transmission of the X chromosomes is shown.
sk is the number of bx -values in each generation. Presumably these proportions were overlooked previously because
of the predominating way of observing descendants. The biometric
and biostatistics structure of the Mendelian laws is after all
mostly directed toward the future-oriented question "where
to?". The question "from where" is less modern,
but nevertheless of equal scientific interest. The bx inheritance probability
values between the female and male ancestors in each generation
also demonstrate the relationship of the Fibonacci numbers, e.g.,
in the seventh ancestral generation: 13 female and 8 male. 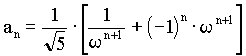 , ,where w represents the "golden ratio" relationship 0.618034… Further: 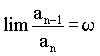 and and 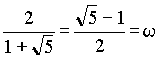 In Geppert's work w appears in
the descendancy in processes of selection and incest. To the
best of my knowledge, it was Rösch (see note 12) who first
referred to the Fibonacci numbers in the ascendency, namely in
an extreme case of an incestual ancestral chart showing continuous
child-parent marriages. The theoretical number of ancestors increases
in the individual ancestral generations according to this sequence.
Further on, Rösch discovered the Fibonacci number sequence
obviously as a physical number of ancestors in the ancestral
chart of bees (see note 13). This chart, however, is in an exceptional
situation because of its peculiar regularity, since each male
bee descends only from a female bee, while each female bee derives
from a pair of parents. Actually, the following ist not part of the main topic we discuss here. This was in appreciation of the 80th birthday of Prof. Dr. Siegried Rösch, Wetzlar. Rösch (see note 14) sees in the number j (the reciprocal value of w), the only positive number whose reciprocal value results from subtraction from 1 as now shown: 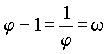 , ,a "world constant": "Our number j has shown such a many-sided significance that it appears worthy of being regarded as a 'world constant', like the Ludolf number p = 3.141592… or the basis of natural logarithms, e = 2.718281.... (both are likewise infinitely long decimal numbers without recurring decimal)." In examples from inanimate and animate nature as well as in works of art, Rösch clearly refers to the Fibonacci numbers and the Golden Ratio relationship. Johannes Keppler called the recognition of this "divine division" a "precious jewel"! We cannot pursue here the further theoretical structure of the X / Y - chromosome transmission in cases of multiple relationship. We cannot even touch upon the practical significance for the breeding of animals, and even plants, of the relationships presented here. All this, as well as possible consequences for the knowledge theory, will have to be followed by those who are more qualified. In Volume 75 we will treat briefly the connections of these findings with descendancy. The original essay is published here for the first time. An english translation is soon to be released. |
||||||||||||||||||||||||||
|