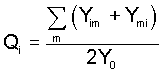|
Let us now introduce gene frequencies pi and qj
(of allele Ai) in the male and female subpopulation,
respectively. Then 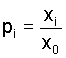 and and 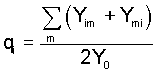 such
that such
that 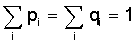 . The recursions (3) imply the fundamental
relations . The recursions (3) imply the fundamental
relations
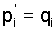
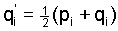 (5) (5)
which can be encountered in different representations in the
literature - at least for the two-allele case (Li 1976; Jacquard
1974; Nagylaki 1977). Furthermore, applying the solution (4)
of the general system to this situation yields the well known
outcome
 , ,
 (6) (6)
exhibiting damped oscillations around the common equilbrium
value
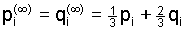
which represents the overall gene frequency in the whole population.
A different point of view is obtained by considering gametic
frequencies Pi and Qi (in males and females)
defined as the proportions of gametes carrying the Ai
allele with respect to all gametes (including those carrying
the Y-chromosome), i.e.
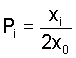 and and 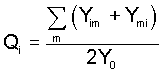
Following this idea we are led to the basic Eqs.
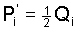
 (8) (8)
Explicit formulas for the gametic frequencies can be derived
in the same way as above and yield the limiting values
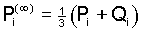 , ,
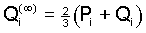 , (9) , (9)
such that

Observing the discrepancy in Eqs. (5) and (8) and, consequently,
in the limiting frequencies (7) and (9), it would seem to be
useful to distinguish between the notions of gene and gametic
frequencies, as both terms are common in two-locus theory. From
the theoretical point of view both cases considered above are
equivalent. Hence they do not represent contradictory theories
but just different models describing the same phenomenon. |
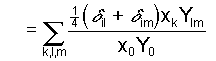
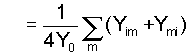 (3a)
(3a)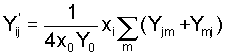 (3b)
(3b)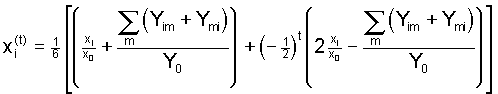 ,
,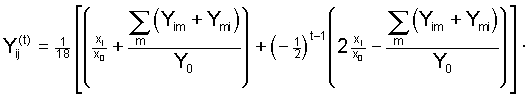
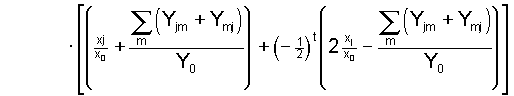 , (4)
, (4) .
.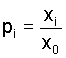 and
and 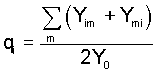 such
that
such
that 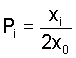 and
and