aus: COMPUTERGENEALOGIE 3 ( 1987 ) H. 7, S. 186-191
| In GENEALOGIE Heft 1 und 2/1984 S. l5ff bzw. 44ff erschien ein Aufsatz von Arndt Richter über: Die Ahnenschaft von Gregor Mendel zu seinem 100. Todestag am 06.01.1984. Darin wird besonders auf den guten Erforschtheitsgrad und die vielen Verwandtenehen hingewiesen. Der Autor weist auf die Möglichkeit hin, diese Ahnenliste als Test für genealogische und nachbarwissenschaftliche Anwendungen von Computergenealogie-Programmen zu verwenden. In der modernen Genetik ist die Computeranwendung selbstverständlich geworden. Daher bringen wir ein wenig "Verwandtschaftsmathematik" von Arndt Richter. |
|
Der o.g. Aufsatz hat im Mendeljahr 1984 eine freundliche Aufnahme gefunden. Begegnungen und Korrespondenz mit Mendelverwandten erfolgten. Dadurch kam ich auch noch in den Besitz der Nachkommentafeln von Gregor Mendels Schwestern. Von beiden Schwestern existiert heute eine umfangreiche Nachkommenschaft. Auch von institutioneller Seite fand der Aufsatz eine günstige Aufnahme, wobei dort vor allem das Ausmaß der verwandtschaftlichen Verflechtung von Gregor Mendels Ahnen überrascht hat. Daher dürfte Mendels Ahnentafel eine erhebliche statistische Bedeutung zukommen, vor allem für die Populationsgenetik und die Demographie. Aus der Korrespondenz mit den biologischen Nachbarwissenschaften habe ich allerdings den Eindruck gewonnen, daß sich bis heute noch kein brauchbares EDV-Programm zur Berechnung der biologischen (genetischen) Verwandtschaft von komplexen Verwandtenehen durchsetzen konnte. Das bei Albert Jacquard (1974) 1) erwähnte IBM-Computerprogramm zur Berechnung von Verwandtschafts- bzw. Inzuchtkoeffizienten scheint ein "Inselverfahren" geblieben zu sein. [ geschrieben August 1984! ]. Besonders erfreulich war es daher, daß mein Aufruf, die Ahnentafel Mendels als Modell für Computerprogramme für genealogische und nachbarwissenschaftliche Zwecke zu verwenden, nicht ohne Echo geblieben ist. M. Sigmund (Institut für Medizinische Statistik, Dokumentation und Datenverarbeitung der Universität Bonn) schickte mir im Juni 1984 eine DIN A3 Computergrafik von Mendels Ahnen, die in verkleinerter Form auf Seite191 zu sehen ist. Diese Grafik enthält für einen Teil von Mendels Ahnen Vor- und Familienname, Personensymbol (Quadrat oder Kreis), Abstammungslinien, Ahnennummer (leider zunächst nur eine!) sowie die Lebensdaten. Die Grafik geht dabei stammbaumartig von Mendels 10-fachem Ahnenpaar Kaspar Pietsch oo N.N. Kuntschig aus. Diese genealogische Computergrafik wurde mittels eines von M. Sigmund entwickelten Plotter-Programmes erstellt, das bereits 1983 als PEDPLO (a PEDigree PLOt Program) vorgestellt worden war 2). Hervorgehoben sei vor allem noch, daß Kurt Ewald, München, mit dem von ihm entwickelten Mikrocomputer-Programm zur Berechnung der gb- und b-Werte von Verwandtenehen meine manuell berechneten Ergebnisse für die Verwandtenehe von Mendels Eltern exakt bestätigen konnte. Weiterhin enthält diese EDV-Berechnung einen Listenausdruck mit allen 64 Verwandtschaftswegen (als Ahnennummernfolge), die biologisch hierfür relevant sind. Als "Nebenprodukt" fielen noch die analogen Berechnungen für die Verwandtenehen von Gregor Mendels Großeltern und Urgroßeltern mit ab. Es mag daher nun gerechtfertigt sein, meine 1983 manuell berechneten Statistikwerte zu Mendels Ahnenschaft hier erstmals zu veröffentlichen. Zu Vergleichs-, aber auch zu Kontrollzwecken sind diese Statistikwerte sicherlich für manche Genealogen, aber auch für den einen oder anderen Naturwissenschaftler von Interesse. Die Terminologie und Notation der Kennwerte folgt meist den bewährten methodischen Arbeiten von Siegfried Rösch. Auf die Technik der Berechnung kann hier nicht eingegangen werden. Der deutsche Leser muß auf die wertvollen Arbeiten von Wilhelm Ludwig (1944) 3) und Siegfried Rösch (1955, 1977) 4) hingewiesen werden. Während Ludwig auf den Arbeiten des amerikanischen Populationsgenetikers Sewall Wright (1922) aufbaut, stützt sich Rösch bei der biologischen Verwandtschaftsberechnung vor allem auf Geppert und Koller (1938). An Röschs "Quantitativer Genealogie" (1955) sollte m.E. auch der Genetiker nicht vorbeigehen, der sich um eine präzise Begriffsbildung innerhalb des verwandtschaftswissenschaftlichen Teils der Populationsgenetik bemüht. Auch auf zwei sehr wertvolle demographisch-genealogische Arbeiten von Hermann v. Schelling (1944, 1945) 5) muß hier noch hingewiesen werden, da v. Schelling dort auf wahrscheilichkeits-statistischem Wege Ahnenimplex-Modelle in Abhängigkeit von der Bevölkerungsgröße (Heiratskreise) abgeleitet hat. In seiner Arbeit von 1945 entspricht dabei das Modellbeispiel mit dem größten Implexwert (kleinster Heiratskreis) dem Ahnenimplexwert von Gregor Mendel überraschend gut. Von einer ebenfalls publizierten bäuerlich-bodenständigen Ahnenschaft aus dem Darmstädter Raum (Proband: Änne Ullrich, geb. 1930)6) werden hier zum Vergleich die analogen statistischen Kennwerte, die ich bereits 1982 berechnet hatte, mit angegeben. Frau Ruth Hoevel, Marburg, sei auch hier sehr für ihre Bemühungen gedankt, mir daß genealogische Material damals für meine Studien zur Verfügung gestellt und erweitert zu haben. Ich begrüße es, die vor über 2 Jahren abgefaßten "statistischen Ergänzungen zur Ahnenschaft von Gregor Mendel" in der COMPUTERGENEALOGIE veröffentlichen zu können. Der "Aufruf", die Mendel-Ahnentafel als methodisches Testbeispiel für verschiedene Computerprogramme zu verwenden (GENEALOGIE 1/1984 S.22) sei an dieser Stelle noch einmal wiederholt. Die Leser unserer Zeitschrift werden wohl zunächst an einem Programm zur Implexberechnung am meisten interessiert sein, bzw. sich ein solches aufgrund ihrer technischen Möglichkeiten selbst erstellen wollen. Als Hilfe für diesen Zweck werden daher noch Tabelle 3 und Tabelle 4 nachgetragen. Die Ahnenstämme in Tabelle 3 entsprechen dabei der Kennzeichnung der Ahnenliste in GENEALOGIE 2/1984, S. 44-56. Das Prinzip der Implex-Berechnung dürfte aus beiden Tabellen zweifelsfrei hervorgehen. Diese Methode hat sich bei der eigenen manuellen Berechnung - auch bei komplexeren Verflechtungen! - gut bewährt. Bei verwandtschaftlichen Zweifelsfällen wird es manchmal nützlich sein, sich die Verflechtungen aufzuzeichnen bzw. anhand der Grafik in GENEALOGIE 1/1984 S.16-17 vor Augen zu führen. Besonders gilt dies für die sogenannten "Kettenehen" mit den Ahnenhalbgeschwistern. In einer der nächsten Nummer dieser Zeitschrift möchte ich versuchen, noch einige prinzipielle und zeichnerische Hinweise für Möglichkeiten zur grafischen Darstellung der Ahnenverflechtungen zu geben (Plotterprogramme). |
|
Literatur:
|
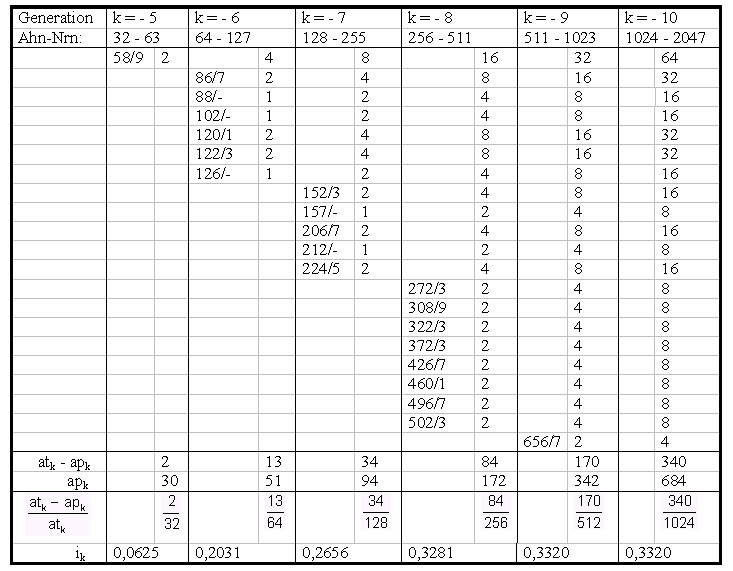
| k | = | Nummer einer Generation; die des Probanden selbst wird als k = 0 angenommen; die Generationen der Vorfahren werden negativ gezählt, die der Nachkommen positiv |
| atk | = | theoretische Anzahl der Ahnen in der k-ten Generation = 2-k (hier ist berücksichtigt, daß k in der Ahnentafel negativ ist) |
| apk | = | physische Anzahl der Ahnen in der Generation k bei Ahnenimplex, dabei wird jede Person, die in der Ahnentafel mehrfach vorkommt, nur einmal gezählt, und zwar jeweils bei ihrer niedrigsten Ahnennummer |
| ik | = |
Ahnenimplex ("Ahnenverlust") in der k-ten Generation
der Ahnentafel = (atk - apk)/atk |
| a'tk | = | unvollständig bekannte theoretische Anzahl der Ahnen in der k-ten Generation infolge Lückenhaftigkeit der Forschung (bei Vollzählung aller Ahnen, deren Identität irgendwie ermittelt ist) |
| a'pk | = | desgl. für unvollständig bekannte physische Anzahl der Ahnen in der k-ten Generation (bei Vollzählung aller Ahnen, deren Identität irgendwie ermittelt ist) |
| rtk | = | Anteil der bekannten theoretischen Ahnen = a'tk/atk |
| z | = | Anzahl der Verwandtschaftswege zwischen zwei Individuen |
| b | = | mittlerer biologischer Verwandtschaftsanteil zweier Individuen = 2-gb |
| gb | = | biologischer Verwandtschaftgrad zweier Individuen = - 2log b = - 3,3219 log b; die einzelnen Verwandtschaftsgrade wurden nach Rösch "symbolisch-komprimiert" dargestellt. Dabei bedeuten die Zahlen keine Potenzen im arithmetischen Sinne, sondern geben die Häufigkeit des Verwandtschaftsgrades (der Grundzahl) wieder: 1715 bedeutet 15-mal im 17. Grad verwandt, zahlenmäßig = 15*2-17 |
| g'b | = | biologischer Verwandtschaftsgrad bei mehrfacher Verwandtschaft (summarischer biologischer Verwandtschaftsgrad) = -2logS b |
| g''b | = | kleinster ganzzahliger biologischer Verwandtschaftsgrad (reine Rechengröße) |
| g"'b | = | reduzierter biologischer Verwandtschaftsgrad (reine Rechengröße) |
| gbs | = | Schwerpunktwert des biologischen Verwandtschaftsgrades (arithmetisches Mittel der Einzelwert) |
| f | = | Inzuchtkoeffizient = b/2 |
| Gregor Mendel (1822-1884) | Änne Ullrich (*1930) | ||||||||||||
| Ahnenimplex | Erforschtheitsgrad | Ahnenimplex | Erforschtheitsgrad | ||||||||||
| k | atk | apk | ik | a’tk | a’pk | rtk | apk | ik | a’tk | a’pk | rtk | ||
| -1 | 2 | 2 | 0,00 | 2 | 2 | 1 | 2 | 0.00 | 2 | 2 | 1 | ||
| -2 | 4 | 4 | 0,00 | 4 | 4 | 1 | 4 | 0.00 | 4 | 4 | 1 | ||
| -3 | 8 | 8 | 0,00 | 8 | 8 | 1 | 8 | 0.00 | 8 | 8 | 1 | ||
| -4 | 16 | 16 | 0,00 | 16 | 16 | 1 | 16 | 0.00 | 16 | 16 | 1 | ||
| -5 | 32 | 30 | 0,06 | 32 | 30 | 1 | 32 | 0.00 | 32 | 32 | 1 | ||
| -6 | 64 | 51 | 0,20 | 60 | 49 | 0,94 | 61 | 0.05 | 63 | 60 | 0,98 | ||
| -7 | 128 | 94 | 0,27 | 97 | 69 | 0,76 | 111 | 0.13 | 102 | 85 | 0,80 | ||
| -8 | 256 | 172 | 0,33 | 93 | 45 | 0,36 | 209 | 0.18 | 134 | 90 | 0,52 | ||
| -9 | 512 | 342 | 0,33 | 58 | 21 | 0,11 | 395 | 0.23 | 143 | <78 | 0,28 | ||
| -10 | 1024 | (684) | (0,33) | 27 | 8 | 0,03 | (790) | (0.23) | 151 | <69 | 0,15 | ||
| -11 | 2048 | - | - | 5 | 3 | 0,00 | - | - | 98 | <71 | 0,05 | ||
| -12 | 4096 | - | - | 1 | - | 0,00 | - | - | 58 | <48 | 0,01 | ||
| 8190 | 403 | 255 | 7,20 | 811 | <563 | 7,79 | |||||||
|
|
|
|
| 1. autosomale Verwandtschaft zwischen den Eltern der Probanden (auf die Normalchromosomen bezogen) | ||
|
z = |
|
|
|
b = |
|
|
|
gb = |
|
|
|
|
||
|
g’b = |
|
|
|
g’’b = |
|
|
|
g’’’b = |
|
|
|
gbs = |
|
|
|
gbs - g’b = |
|
|
| 2. x-chromosomale Verwandtschaft zwischen den Eltern der Probanden (auf die X-Chromosomen bezogen) | ||
|
zx = |
|
|
|
bx = |
|
|
|
gbx = |
|
|
| 3. Inzuchtkoeffizienten der Probanden (autosomal und x-chromosomal) | ||
|
f = |
|
|
|
fx = |
|
|
| (nur bei Frauen!) für Mendels Schwestern: 0,00781 | ||
|
|
|
|
| Ahnenstämme |
|
|
| a.) Vollgeschwister | ||
| Weiß Ia / Ib |
|
|
| Blaschke Ib / Id |
|
|
| Blaschke Ic / Ie |
|
|
| Münster Ib / Ia |
|
|
| Blaschke Ic / If |
|
|
| Ertel Ib / Ia |
|
|
| Brosch Ia / Ib [ siehe auch c.)] |
|
|
| Blaschke Ia / Ic / Ig |
|
|
| Schreiber Ib / Ia |
|
|
| Schwirtlich Ia / Ib |
|
|
| Kasper Ib / Ia [ siehe auch b.) und c.)] |
|
|
| Pietsch Ia / Ib /ic |
|
|
| Schlosser Ib / Ia |
|
|
| Kahlig Ib / Ia |
|
|
| b.) Halbgeschwister mit gemeinsamem Vater | ||
| Blaschke Ia / Ib |
|
|
| Kuntschig Ia / Ib |
|
|
| Ertel Ia / Ic |
|
|
| Kasper Ic / Ib / Ia [ siehe auch a.)] |
|
|
| c.) Halbgeschwister mit gemeinsamer Mutter | ||
| Kaspar Ic / Brosch Ia / Ib [ siehe auch a.)] |
|
|

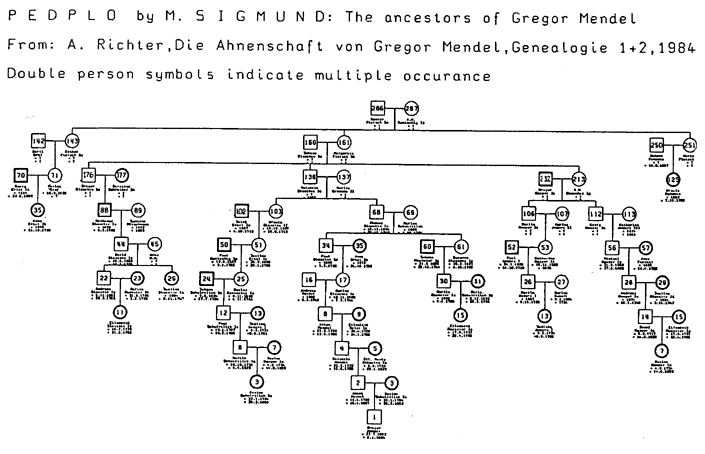
| Für die vollständige Darstellung der verwandtschaftlichen Verflechtung der Ahnen von Gregor Mendel (Ahnentafelausschnitt) siehe hier; für den daraus berechneten Verwandtschaftskoeffizienten f von Gregor Mendel siehe hier. |